Cherent Manipulation of Coupled Electron Spins in Semiconductor Quantum Dots

Jiheng Duan, jiheng.duan@rochester.edu, 09/03/2023

Paper Information

• DOI: 10.1126/science.111.6955
• Date: 30, Sept., 2005
• Author: J. R. Petta, A. C. Johnson, J. M. Taylor, E. A. Laird, A. Yacoby, M. D. Lukin, C. M. Marcis, M. P. Hanson, A. C. Gossard

Motivation

1. Using electrons as qubits in semiconductor devices to encode information.
2. Achieve qubit initialization, measurement, coherent control ($\sqrt{\text{SWAP}}$ gate)
3. Characterizing $T_1$ and $T_2$.
4. Analyzing decoherence sources.

Spin manipulation and measurement

Devices infor

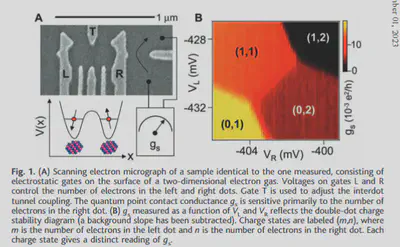
See Fig.1.

• Material: GaAs/AlGaAs (small electron effective mass).
• Fabrication: Molecular beam epitaxy.
• Density of electron gas: $n \sim 2\times 10^{11} \text{cm}^{-2}$ under $100 \text{nm}$ of the surface.
• Electron temperature: $T_e\sim 135 \text{mK}$.
• Two tunnel barries (control left gate voltage $V_L$ and right gate voltage $V_R$) control the detuning to allow electron move in or out the dot.
• Detuning parameter $\epsilon \propto V_R - V_L$.
• The detuning parameter $\epsilon$ controls the system state.

Qubit infor

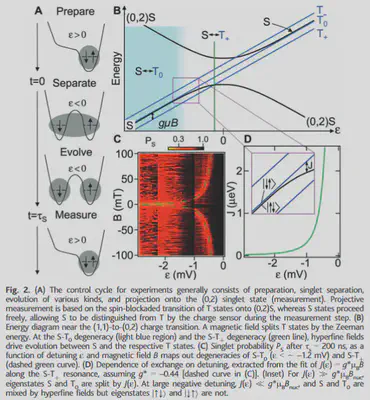
See Fig.2.

• System cycle: shown in Fig.2A.
• Computational subspace: $S$ and $T_0$ ($m_s = 0$), which are $(|\downarrow\uparrow\rangle - |\uparrow\downarrow\rangle)/\sqrt{2}$ and $(|\downarrow\uparrow\rangle + |\uparrow\downarrow\rangle)/\sqrt{2}$.
• Measurement: using quantum point contact sensor. Details see next section.
• Manipulation: by change detuning $\epsilon$; A fixed z-direction B-field to induce Zeeman splitting.
• Four significant region (see Fig.2B):

• $\epsilon>0$: system at $(0,2)S$, two spin are in one potential wall. $(m,n)$ is a notation of charge state, where $m,n$ represents the number of electrons inside the left and right dots, respectively.
• $\epsilon_{T+} \approx \epsilon < 0$: $S$ state resonant with $T_+$ state.
• $\epsilon_{T+} > \epsilon$: $S$ state hybrids with $T_0$, with a exchange interaction strength $J(\epsilon)$.
• $\epsilon « J(0)$: Avoid crossing induced by spin-nuclei hyperfine interaction, with spacing $J(\epsilon) = g^*\mu_B B_{nuc} \rightarrow 0$. In this case, $S$ and $T_0$ are mixed by hyperfine field. The eigenstates of hyperfine interaction $|\downarrow\uparrow\rangle$ and $|\uparrow\downarrow\rangle$ are not mixed. See Fig.2D

• System Hamiltonian $$ H = \begin{bmatrix} J(\epsilon) & \Delta B^{z}{\text{nuc}} \ \Delta B^{z}{\text{nuc}} & 0 \end{bmatrix} $$ where $\Delta B^{z}{\text{nuc}} $ is teh difference in random hyperfine fields along the applied external B-field direction. In this paper, $B{\text{nuc}} \sim 1$ to $5$ mT.

Measurement

Measurement, which is a projective measurement, is based on the spin-blockaded transition technique. A Singlet-Triplet qubit state (spin state) measurement is achieved by switching the detuning $\epsilon$ from negative value to positive, which will map $S$ to $(0,2)S$ charge state and $T_0$ (or $T_\pm$, depends on which state you are considered as computational state) remain in $(1,1)$, a spin-blocked configuration. The difference in $(0,2)$ and $(1,1)$ can be distinguished by quantum point contact (QPC), shown in the region diagram in Fig.1B.

The QPC sensor is used to distinguish charge states, which says the charge state (or more specificity, the number of electrons inside the neighbor quantum dots) of the electron inside a quantum dots will affect the conductance $g_s$ of a gate, indicated by the black arrow in Fig.1A.

Single qubit manipulation

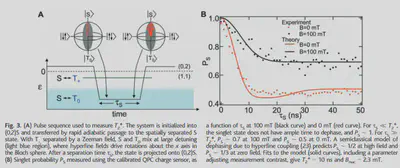
Bloch sphere

Shown in Fig.3A, we choose $|0\rangle = |S\rangle$ and $|1\rangle = |T_0\rangle$. The eigenstates of hyperfine interaction are place at two points on the intersection points of sphere and x-axis.

Spin SWAP

Pulse sequences are shown in Fig.3

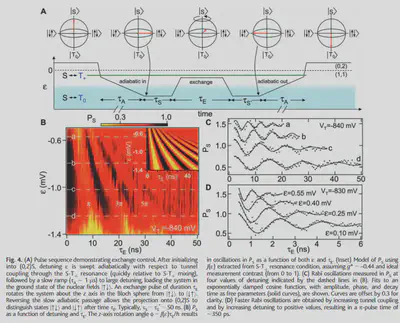
Rabi oscillations in $|\downarrow\uparrow\rangle$ and $|\uparrow\downarrow\rangle$ basis

Pulse sequences are shown in Fig.4

T2 measurement, spin echo

Pulse sequences are shown in Fig.5

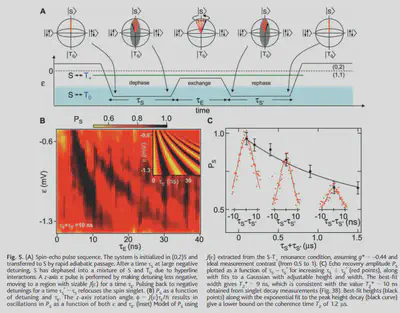
Decoherence

Spin qubits have a long $T_1$ which is about tens of ms. But it has a really short $T_2$, which is measured by spin echo in this paper wich a value $T_2 \sim 10 ns$.

The reason for such short dephasing time is due to the hyperfine interaction between spin and nuclei.