Characterizing temperature and strain variations with qubit ensembles for their robust coherence protection

Jiheng Duan, jiheng.duan@rochester.edu, 09/14/2023

Paper Information

• DOI: 10.1103/PhysRevLett.131.043602
• Date: 25, July., 2023
• Author: Guoqing Wang, Ariel Rebekah Barr, Hao Tang, Mo Chen, Changhao Li, Haowei Xu, Andrew Stasiuk, Ju Li, and Paola Cappellaro

Motivation

1. Solid-state spin defects (NV center in diamond here) suffer from dephasing due variations of intrinsic quadrupole and hyperfine interactions.
2. Using electron spins to refocus variations of interactions (quadrupole and hyperfine) to achieve long nuclear spin free evolution. Known as unbalanced echo.
3. This unbalanced echo technique and be used to sensing temperature and strain variations in materials with nanoscale resolution.

Unbalanced echo

• It involves flipping an ancillary qubit (here the N-V electronic spin) midway through the free precession period of the target qubit (here the nitrogen nuclear spin).

• The flip time $\tau$ is asymmetric - it does not split the free precession time t into two equal halves, hence “unbalanced”.

• This echo sequence cancelles out low-frequency noise from interaction variations, acting like a spin echo.

• However, it preserves the useful quantum phase information accumulated during the free precession, unlike a regular spin echo.

Setup system

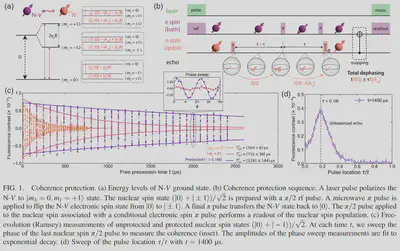
• The system diagram and energy levels are shown in Fig.1 (a).
• The nuclear spin (n spin) is qubit and N-V center electron spin (e spin) is bath.
• e spin state is switched between $|m_S = 0\rangle$ and $| m_S = \pm 1 \rangle$.
• n spin contains single quantum (SQ) transitions between $|m_I = 0\rangle$ and $|m_I = \pm \rangle$ which have six different frequencies: $\omega_{1,2} |Q| \pm |\gamma_n B|$, $\omega_{3,4} = |Q| \mp |A_{zz}| \pm |\gamma_n B|$, and $\omega_{5,6} = |Q| \pm |A_{zz}| \pm |\gamma_n B|$, corresponding to the electron spin state $|m_S = 0\rangle$, $|m_S = -1\rangle$, and $|m_S = +1\rangle$, respectively.
• In a magnetic field $B$ aligned with the N-V center, the Hamiltonian of nuclear spin is given by $$ H_n = Q I^2_z + m_S A_{zz}I_z + \gamma_n B I_z $$ where $I_z$ is the spin-1 $z$ operator, and we assume the N-V electronic spin is in its eigenstate $|m_S\rangle$.

Pulse sequence

• The pulse sequence are shown in Fig.1 (b).
• The N-V center electron are polarized to state $|m_S = 0, m_I = +1\rangle$ by a laser pulse.
• The nuclear spin state $(|0\rangle + |\pm 1\rangle)/\sqrt{2}$ is prepared with a $\pi/2$ pulse (notice that ``$m_I = $’’ is omitted here for simplicity).
• Suppose we prepare nuclear spin state $(|0\rangle + |- 1\rangle)/\sqrt{2}$ and drive the spin state between $|m_S = 0\rangle$ and $|m_S = \pm 1\rangle$.
• The free evolution of nuclear spin state after time $t$ is given by $|\psi(t)\rangle = (|0\rangle + e^{i\phi}|-1\rangle)/\sqrt{2}$ with an accumulated quantum phase $\phi = \omega t$.
• At time $t - \tau$, we apply a $\pi$ pulse on the spin state, flipping the spin state from $|m_S = 0\rangle$ to $|m_S = \pm 1\rangle$, turning the level frequency from $|Q| - |\gamma_n B|$ to $|Q| \mp |A_{zz}| - |\gamma_n B|$.

• The accumulated phase and dephasing till now is $ \phi_0 + \delta\phi = -(|Q|-|\gamma_n B|)(t - \tau) + (\delta|Q| + \gamma_n \delta|B|)(t - \tau) $ where $\delta$ means variation. Why there is a minus sign behind $\phi_0$ ??? And why there is a plus sign behind the $\delta B$ term ???

• At time $t$, we apply another $\pi$ pulse on the spin state, flipping the spin state back to $|m_S = 0\rangle$. turning the level frequency back to $|Q| - |\gamma_n B|$.

• The accumulated phase and depasing in time interval $[t-\tau, t]$ is $\phi_0’ + \delta\phi’ = -(|Q| \mp |A_{zz}| - |\gamma_n B|)\tau + (\delta|Q| \mp \delta|A_{zz}| - \gamma_n \delta|B|)\tau$.

• Assume the flipped electron state is $|\m_S = +1\rangle$. The total accumulated phase and dephasing is given by $\phi = \phi_0 + \phi_0’ + \delta \phi + \delta \phi’$.
• In optically addressed solid-state spin ensembles, the laser heating introduces temperature variations $\delta T$. This temperature variation will induce the variation in quadrupole and hyperfine interaction (assume the variation of the magnetic file $\delta B$ is minimized when designing the experimental setup, and the small gyromagnetic ratio $\gamma_n/\gamma_r \sim 10^{-4}$ introduces negligible coupling to the magnetic noise).
• Therefore, one correlation can be made by expressing $\delta Q = \alpha_Q \delta T$ and $\delta A_{zz} = \alpha_A \delta T$.
• The total phase accumulation and dephasing becomes $$ \begin{aligned} \phi (\delta T) &= \varphi_0 + \delta\varphi \ &= -t Q + \tau A_{zz} + \gamma_n B t - (t\alpha_Q - \tau\alpha_A)\delta T, \end{aligned} $$ where $\varphi = -t Q + \tau A_{zz} + \gamma_n B t$ and $\delta \varphi = - (t\alpha_Q - \tau\alpha_A)\delta T$.
• If the pulse location $\tau/t$ is set to the ratio $\alpha_Q/\alpha_A$, the noise (dephasing) $\delta \varphi$ can will be completely canceled while the static part $\varphi_0$ still remain sensitive to the magnetic field.

Fitting, get $T_2^* $

• We use a Ramsey type pulse on the n spin, and map the dephasing on to the e spin and perform a measurement.
• The Ramsey signal $$ S(t) = [1 + \cos(\omega t)]/2, $$ where $\omega = \omega_0 + \delta \omega$. The $\delta \omega$ satisfies a zero-mean Lorenzian distribution with a half-width $\sigma = 1/T_2^$, the signal has an exponential decay envelope $\langle cos(\omega t) \rangle = \cos(\omega_0 t) e^{-t/T_2^}$ characterizing the loss of quantum information.
• By sweeping the phase $\phi$ and free evolution time $t$, we could measured the curve in Fig.1 (c).
• Fig.1 (d) shown a sweep of pulse location $\tau/t$ with $t=1400 \mu s$, where an unbalanced echo signal is observed at $\tau/t = 0.18$.

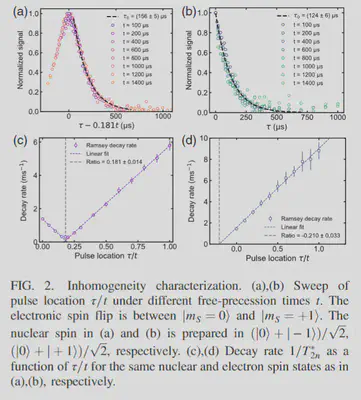
Characterization of temperature and stain distribution

• Based on the discussion of frequency noise $\delta \omega$, by probing the material dependent ratio $\alpha_Q/\alpha_A$, it can be used to characterize the temperature distribution in the material by analyzing the shape and decay constant in the unbalanced echo and free-evolution measurements.
• The Lorentzian distribution of the temperature with half-width $\sigma_T$, the dephasing factor becomes $$ e^{-t/T_{2n}^*} = ee^{-|t\pm (\alpha_Q/\alpha_A)t||\alpha_A| \sigma_T}, $$ for nuclear spin state $(|0\rangle + |\pm 1\rangle)/\sqrt{2}$, respectively.

Refocusing strong noise variations

C.f. Sec. Refocusing strong noise variations.