Microwave-driven iSWAP-like gate for fixed-frequency superconducting transmon qutrits

Jiheng Duan, jiheng.duan@rochester.edu, 10/01/2023

Paper Information

• DOI: 10.1103/PhysRevA.108.032615
• Date: 26, Sept., 2023
• Author: Peng Xu, Qingli Jing, Peng Zhao, Yang Yu

Motivation

1. High fidelity, zz-free, low leakage all microwave two qutrit entanglement gate, iSWAP like.

Computational subspace and coupling

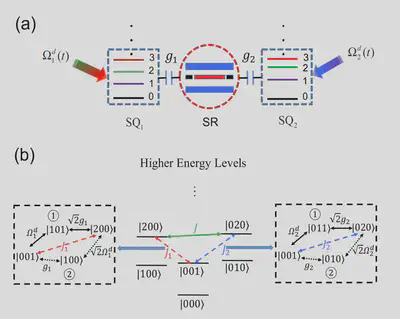
• Transmon-Resonator-Transmon system
• System Hamiltonian

$$ H_s = \sum_j \left( \omega_j q_j^\dagger q_j + \frac{\alpha}{2} q^\dagger_j q^\dagger_j q_j q_j \right) + \omega_r c^\dagger c + \sum_j g_j(q^\dagger_j + q_j)(c^\dagger + c) $$

• Driving term

$$ H_d = \sum_j \Omega_j \cos(\omega_j^d)(q^\dagger_j + q_j) $$ where $\omega_j^d \approx 2\omega_j + \alpha_j - \omega_r$, $\Omega_j$ is the pulse amplitude.

• Effective Hamiltonian is obtained by doing the Schrieffer-Wolf transformation twice, where we get effective coupling between Qj-R ($J_j$) and Q1-Q2 (e.g., virtual photon exchange through state $|001\rangle$, $J_{001}$), respectively. See Eq.(4) and Eq.(5) in the paper.

$$ H_I = J_{001}\left( |200\rangle\langle020| + |020\rangle\langle200| \right) $$ Where the reduced two-level qutrit is still far detuned from the resonator $|2\omega_j + \alpha_j - 2\omega_r|$.

iSWAP like gate

The entanglement gate looks like $$ i\text{SWAP}_\text{like} = \left[ \begin{matrix} 1 & 0 & 0 & 0\ 0 & 0 & -i & 0\ 0 & -i & 0 & 0\ 0 & 0 & 0 & e^{-i\phi} \end{matrix} \right] $$

Static ZZ

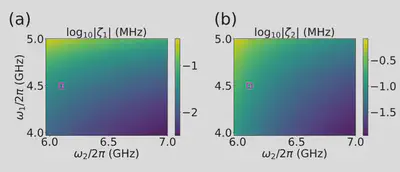
• Suppressing to less than 50 kHz for the first excited state, shown in (a)
• Suppressing to as small as 50 kHz for the second excited state, shown in (b).
• Trade-off should be made from coupling strength ($g_j$) and ZZ coupling (choice of $\omega_1$, $\omega_2$).
• High coupling strength decrease gate time, but increase ZZ couping.

Driving Pulse

• The pulse is consisted with a cosine oscillating carrier and a Gaussian envelope, which provides smooth rising (lowering) edges.
• The microwave pulse:

$$ \Omega_j^d(t) = \Omega_j G_j^d(t) \cos\left( \omega_j^d t \right) $$ where $$ G_j^d(t) = \left{ \begin{array}{ll} \frac{e^{-(t - t_r)^2/(2\delta^2)} - e^{-t_r^2/(2\delta^2)}}{1 - e^{-t_r^2/(2\delta^2)}}, & t \le t_r;\ 1 & t_r< t < t_p - t_r;\ \frac{e^{-(t - (t_p - t_r))^2/(2\delta^2)} - e^{-t_r^2/(2\delta^2)}}{1 - e^{-t_r^2/(2\delta^2)}}, & t - t_r \le t \le t_p;\ 0 & others \end{array} \right. $$

• The parameters of a exampled simulation can be found in TABLE I. and TABLE 2. The gate time of that simulation is $t_g = 280 ns$ when $\delta = 30 ns$ (which is the variance of the Gaussian, controls the width of the Gaussian).

Gate Fidelity

• Improved simulation result by increasing the ramp time $t_r$: $F \approx 99.9%$
• The gate fidelity increase with the quality factor of the resonator. See Fig.6 (c).
• The decoherence affected gate error are shown in Fig.6 (c) and (d).
• The discussion of leakage error is shown in Appendix C.