Demonstration of universal control between non-interacting qubits using the Quantum Zeno effect

Jiheng Duan, jiheng.duan@rochester.edu, 10/09/2023

Paper Information

• DOI: 10.1038/s41534-022-00594-4
• Date: 2022
• Author: E. Blumenthal, C. Mor, A. A. Diringer, L. S. Martin, P. Lewalle, D. Burgarth, K. B. Whaley, and S. Hacohen-Gourgy

Motivation

Using superconducting qubit to demonstrate quantum zeno effect.

Quantum Zeno effect

An effect lies on the boundary between coherent and incoherent control of a quantum system, in which frequent measurements effectively freeze the system dynamics, holding the system at an eigenstate of the measurement observable.

Method

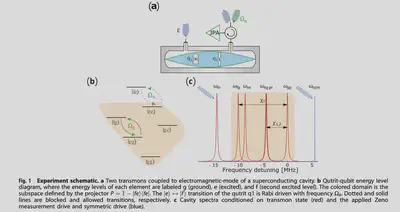
• A qutrit and a qubit inside a resonator, no interaction between qutrit and qubit.
• See Fig. 1

• $q_1$: qutrit, $q_2$: qubit
• $\varepsilon$ is the microwave pulse driving the resonator, at frequency $\omega_{fe}$
• $\omega_{fe}$ is the resonator frequency when $|q_1, q_2\rangle = |f,e\rangle$, the dispersive shift.
• $\Omega_R$ is the microwave pulse driving the qutrit state $|e\rangle \leftrightarrow |f\rangle$

• The driving of resonator is effective to be a measurement of the projection operator $P = 1 - |fe\rangle\langle fe|$ (frequently excite the cavity and measure at frequency $\omega_{fe}$, equivalent to frequently apply the measurement of the projection operator $P$).
• The Zeno Hamiltonian becomes

$$ H_{\text{Zeno}} = PHP = i\hbar \frac{\Omega_R}{2} \left( |eg\rangle\langle fg | - | fg \rangle \langle eg | \right) $$ where $H = \frac{1}{2} \hbar \Omega_R \left( |e \rangle\langle f| - |f \rangle\langle e| \right) \otimes \left(g | \rangle\langle g| + |e \rangle\langle e| \right)$

• We see the Zeno Hamiltonian describe a Rabi between $|eg\rangle \leftrightarrow |fg\rangle$, and block the $|ee\rangle \leftrightarrow |fe\rangle$ transition.
• This restrict the system into a computational subspace, shown as the color region in Fig. 1(b).
• This can also be done for multiple qubit system. $P = 1 - |feee\cdots\rangle\langle feee\cdots|$

Experiment

• The system Hamiltonian without Zeno drive and Rabi drive is a dispersive Hamiltonian in the interaction picture

$$ H_{\text{disp}}\hbar = \left( \chi_1 |e_1\rangle\langle e_1 | + \chi_2 | e_2 \rangle\langle e_2 | + \chi_f | f \rangle\langle f| \right) a^\dagger a + \alpha_1 |f\rangle\langle f| $$ where $\chi_i$ is the dispersive shift, $\alpha_i$ is the anharmonicity.

• Despite the Zeno drive at $\omega_{fe}$, a symmetric drive which is symmetric to the Zeno measurement drive frequency with respect to $\omega_{eg}$ and $\omega_{ge}$ are added.
• This symmetric drive balances the phase accumulation, such that this no longer generates entanglement.
• The system Hamiltonian with Zeno and symmetric driving under the rotating frame of $\omega_{gg}$ is

$$ H/\hbar = H_{disp}/\hbar + i\varepsilon \left( a e^{-i(\chi_f + \chi_2)t} - a^\dagger e^{i(\chi_f + \chi_2)t} \right) + i\varepsilon \left( a e^{-i(\chi_2 - \chi_f)t} - a^\dagger e^{i(\chi_2 - \chi_f)t} \right) $$

• Experiment result could refer to this paper. Here we skip it.

Residual effects of the Zeno drive

• Refer to the Sec. Residual effect of the Zeno drive
• The coherence will be lost due to measurement-induced dephasing at a rate.
• The Zeno drive only will cause entanglement, which is the reason for adding additional symmetric drive.