Identification of Different Types of High-Frequency Defects in Superconducting Qubits

Jiheng Duan, jiheng.duan@rochester.edu, 10/31/2023

Paper Information

• DOI: 10.1103/PRXQuantum.3.040332
• Date: 2022
• Author: Leonid V. Abdurakhimov, Imran Mahboob, Hiraku Toida, Kosuke Kakuyanagi, Yuichiro Matsuzaki, and Shiro Saito

Motivation

1. Using c-shunt Flux qubit to characterize high frequency TLS
2. Study two types TLS: charge noise and critical current noise
3. Experimentally verify the proposed qubit-TLS interaction model

Background

Some key concepts are collected from Sec.1 of this paper.

1. Possible TLS sources: tunneling atoms, dangling electronic bonds, impurity atoms, and trapped charge states.
2. A junction tunnel barrier is formed of an amorphous layer of aluminum oxide that hosts a large number of TLS defects
3. Normally, it is assumed that the qubit-defect interaction is caused by an electric field coupling between an electric dipole associated with a charge TLS defect and a microwave electric field generated across a Josephson junction
4. Characterizing method: qubit-TLS frequency matching, apply external E-field to change TLS frequency, adding strength
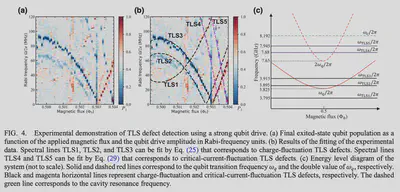
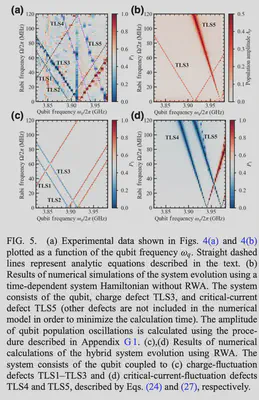
5. Measurement method: measure the avoid-crossing of the qubit frequency spectrum, qubit response to the Rabi drive, measuring qubit’s $T_1$, off-resonant drive (for fixed-frequency qubit, narrow band width: $\pm 25$ MHz)
6. For low-frequency TLS characterization method, the spin-locking pulse sequence (low-frequency spin-locking spectroscopy) method are used, focusing on low-frequency longitudinal nose.
7. This work make a complements to the spin-locking method as the reported method effectively probes a high-frequency transverse noise
8. Also, those population oscillations due to the non-resonant (dispersive) interaction between the qubit and detuned TLS defects can result in additional gate and measurement errors

Key idea of this work

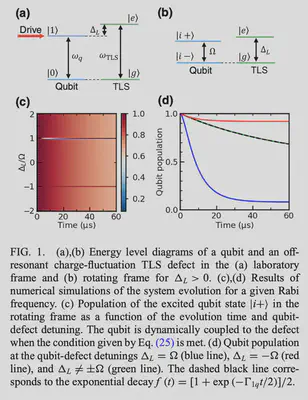
In this paper, they use strong resonant qubit drive method: the relaxation of a strongly driven qubit can be affected by the presence of an off- resonant high-frequency TLS defect due to the dynamic splitting of the qubit transition frequency, caused by the resonant ac Stark effect (Autler-Townes splitting), and the corresponding dynamic matching of qubit and TLS defect frequencies in the rotating frame.

Two types of defects

The total Hamiltonian is given by $$ H = H_q + H_{\text{TLS}} + H_I^{(\mu)} + H_d $$ where $H_q$: qubit hamiltonian, $H_{\text{TLS}}$: TLS Hamiltonian, the interaction term for qubit-TLS interaction, $\mu\in{C,I}$ represents charge and critical current noise.

Qubit Hamiltonian

For a c-shunt flux qubit, its intrinsic Hamiltonian with charge and critical current noise is

$$ H = E_{C_S} (n + \delta n)^2 + 2E_J (1-\cos \phi) \ + \alpha E_J \left( 1 + \frac{\delta I_\alpha}{\alpha I_c} \right) [1+\cos(2\phi + 2\pi \delta f)] $$

where the notation and details can refer to Sec.2 A of this paper (suggested).

The second quantized qubit Hamiltonian is given by

$$ H_q = \hbar \left( \omega_b + \frac{A}{2} \right) b^\dagger+b + \frac{\hbar A}{2}(b^\dagger b)^2 $$ where $$ \hbar A = \frac{8\alpha - 1}{4-8\alpha} E_{C_S}. $$ The qubit frequency is now $\omega_1 = \omega_{01} = \omega_b+A$, and $\omega_{12} = \omega_b +2A$.

TLS Hamiltonian

The intrinsic Hamiltonian of a TLS is given by

$$ H_{\text{TLS}} = \frac{1}{2} \hbar \omega_{\text{TLS}} \sigma_z $$

Qubit-TLS interaction

Charge noise

The standard charge-fluctuation TLS defects

• Interaction type: beam-splitter-type interaction

The qubit-TLS interaction is give by

$$ H_I^{(C)} = i\hbar g_C (b^\dagger + b) $$ where the coupling strength is given by $$ g_C = \frac{1}{2} \delta n_{\text{TLS}} \sqrt{\frac{\omega_b E_{C_S}}{\hbar}} $$ where the charge fluctuation is $\delta n_{\text{TLS}}$

Critical current noise

The TLS defects with a nonlinear coupling to the qubit mediated by critical-current fluctuations.

• Reason: As the thickness of the junction tunnel barrier is nonuniform, the tunneling of Copper pairs occurs through a discrete set nof conductance channels. Fluctuations in the charge configuration of a TLS defect can block on of the conductance channels, resulting in the fluctuations of the critical current

• Interaction type: three-wave-mixing interaction

The qubit-TLS interacting Hamiltonian is given by

$$ H_I^{(I)} = \hbar g_I^{(1)} \sigma_x (b^\dagger + b) + \hbar g_I^{(2)} \sigma_x (b^\dagger + b)^2 $$

where the two coupling strength is given by $$ g_I^{(1)} = -\pi \delta f \frac{\alpha}{\sqrt{1-2\alpha}} \left( \frac{\delta I_{\text{TLS}}}{\alpha I_c} \right) \sqrt{\frac{\omega_b E_J}{\hbar}} $$ and $$ g_I^{(2)} = -\frac{\alpha}{4-8\alpha} \left( \frac{\delta I_{\text{TLS}}}{\alpha I_c} \right) \omega_b $$

In this paper, the qubit is operated at the optimal flux bias point, which means $\delta g \approx 0$. Therefore, the critical current TLS-qubit interaction term is reduced to

$$ H_I^{(I)} = \hbar g_I^{(2)} \sigma_x (b^\dagger + b)^2 $$

Driving term

The Rabi driving term is given by $$ H_d = i\hbar \Omega \cos(\omega_q t) (b^\dagger - b) $$

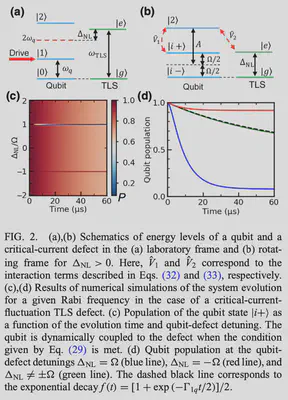
and we treat the system under the interaction picture, there fore the energy level in this system for consider charge noise only and critical current only case are shown in Fig.1 and Fig.2, respectively.

Experiment result

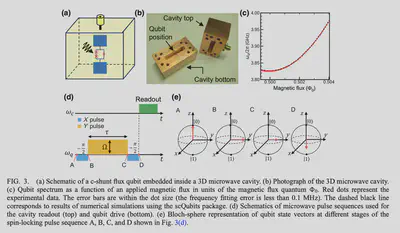
1. Device shown in Fig.3 (a) and (b)
2. The qubit-flux response is shown in Fig3.(c)
3. The measuring method is sending a Ramsy-type pulse on the X-channel, and a Rabi Oscillation on the Y-channel in between the two $\pi/2$ X-pulse, shown in Fig.3(d)
4. The Bloch sphere dynamics are shown in Fig3.(e)